Asymptotic Notation
Consider the example: Given number
n n n
, write a function to find sum of first
n n n
natural numbers.
Some solutions (Python):
def sum1 ( n ):
return n * ( n + 1 ) / 2
Total work done:
c 1 c_{1} c 1
and it is not dependent on
n n n
.
def sum2 ( n ):
sum = 0
for n in range ( n + 1 ):
sum += n
return sum
Total work done: Some constant work and a loop that executes n times:
c 2 n + c 3 c_{2}n + c_{3} c 2 n + c 3
.
def sum3 ( n ):
sum = 0
for i in range ( 1 , n + 1 ):
for j in range ( 1 , i + 1 ):
sum += 1
return sum
The inner loop executes:
once for i = 1
twice for i = 2
thrice for i = 3
So the total work done is:
1 + 2 + 3 + . . . + n = n ∗ ( n + 1 ) / 2 = c 4 n 2 + c 5 n + c 6 1 + 2 + 3 + ... + n \\
= n * (n + 1)/2 \\
= c_{4}{n^2} + c_{5}n + c_{6}
1 + 2 + 3 + ... + n = n ∗ ( n + 1 ) /2 = c 4 n 2 + c 5 n + c 6
It’s a measure of the order of growth of an algorithm in terms of its input size.
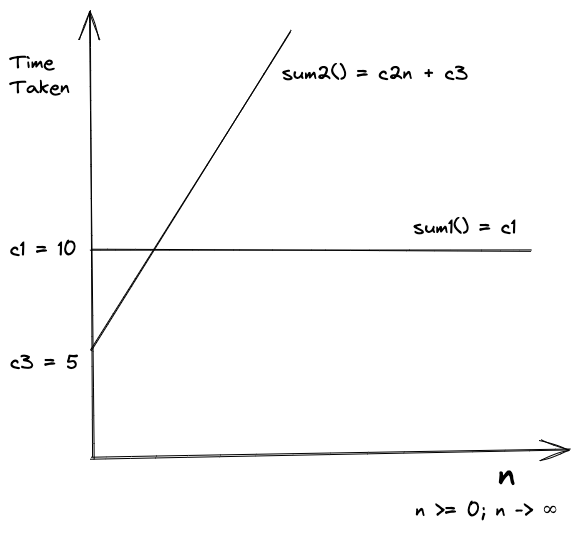
Let’s compare the growth of solutions 1 and 2.
Assuming the values of constants as per the figure below, let’s find
n n n
.
2 n + 5 ⩾ 10 ∴ n ⩾ 2.5 ≈ 3 2n + 5 \geqslant 10 \therefore n \geqslant 2.5 \approx 3 2 n + 5 ⩾ 10 ∴ n ⩾ 2.5 ≈ 3
So, for any
n > = 3 n >= 3 n >= 3
the constant function sum1() will always be faster than sum2().
A function
f ( n ) f(n) f ( n )
is said to be growing faster than
g ( n ) g(n) g ( n )
if
for n ⩾ 0 , f ( n ) , g ( n ) ⩾ 0 lim n → ∞ g ( n ) f ( n ) = 0 \text {for $n \geqslant 0, f(n), g(n) \geqslant 0 $} \\
\lim\limits_{n \to \infty} \frac{g(n)}{f(n)} = 0 for n ⩾ 0 , f ( n ) , g ( n ) ⩾ 0 n → ∞ lim f ( n ) g ( n ) = 0
Example:
f ( n ) = n 2 + n + 6 g ( n ) = 2 n + 5 lim n → ∞ 2 n + 5 n 2 + n + 6 dividing by highest term i.e. n 2 lim n → ∞ 2 / n + 5 / n 2 1 + 1 / n + 6 / n 2 with n tending to ∞ lim n → ∞ 0 + 0 1 + 0 + 0 = 0 f(n) = n^2 + n + 6 \hspace{20px} g(n) = 2n + 5 \\
\lim\limits_{n \to \infty} \frac{2n + 5} {n^2 + n + 6} \\
\small \text{dividing by highest term i.e. } n^2 \hspace{10px}
\lim\limits_{n \to \infty} \frac{2/n + 5/n^2} {1 + 1/n + 6/n^2} \\
\small \text{with n tending to } \infty \hspace{10px}
\lim\limits_{n \to \infty} \frac{0 + 0}{1 + 0 + 0} = 0 f ( n ) = n 2 + n + 6 g ( n ) = 2 n + 5 n → ∞ lim n 2 + n + 6 2 n + 5 dividing by highest term i.e. n 2 n → ∞ lim 1 + 1/ n + 6/ n 2 2/ n + 5/ n 2 with n tending to ∞ n → ∞ lim 1 + 0 + 0 0 + 0 = 0
So, if
f ( n ) f(n) f ( n )
and
g ( n ) g(n) g ( n )
represent time complexity of algorithms i.e. order of growth,
g ( n ) g(n) g ( n )
is a better algorithm.
Direct way to find out the order of growth
Ignore lower order terms.
Ignore leading constants.
Faster growing function dominates a slower growing one.
Common dominance relations:
C < loglog n < log n < n 1 / 3 < n 1 / 2 < n < n 2 < n 3 < 2 n < n n C < \text {loglog } n < \text {log } n < n^{1/3}< n^{1/2} < n < n^2 < n^3 < 2^n < n^n C < loglog n < log n < n 1/3 < n 1/2 < n < n 2 < n 3 < 2 n < n n
Asymptotic Notations and Best, Average and Worst Cases
Best, Average and Worst Cases
Let’s Consider some examples:
def nsum ( arr , n ):
sum = 0
for i in range ( n ):
sum += arr [ i ]
return sum
This function is linear .
def nsum ( arr , n ):
if n % 2 != 0 :
return 0
sum = 0
for i in range ( n ):
sum += arr [ n ]
return sum
Best Case : When n is odd, it’s going to take constant time.Average Case : Often it’s impractical to calculate unless you know all the inputs that will be provided to the algorithm all the time.Worst Case : When n is even it will be linear .
Worst Case is considered the most important case for algorithm analysis.
Cases are not related to notations . You can use the any notation for any case.
Big O : Represents exact or upper bound i.e. order of growth.Big Theta (𝛳) : Represents exact bound.Big Omega (Ω) : Represents exact or lower bound.
Big O is the most common notation used.
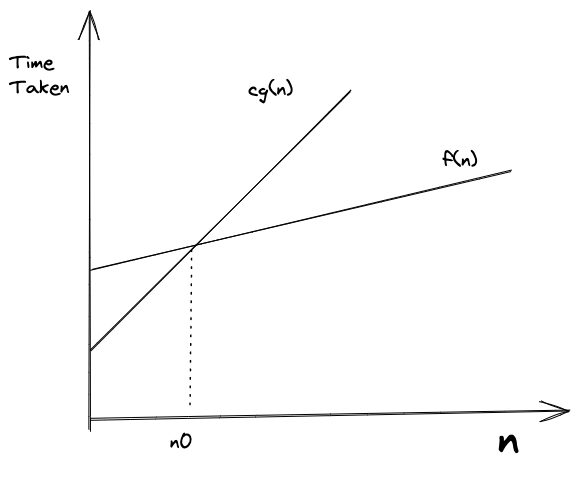
f ( n ) = O ( g ( n ) ) f(n) = O(g(n)) f ( n ) = O ( g ( n ))
if and only if there are exact constants
c c c
and
n 0 n_0 n 0
such that
f ( n ) ⩽ c g ( n ) f(n) \leqslant cg(n) f ( n ) ⩽ c g ( n )
for all
n ⩾ n 0 n \geqslant n_0 n ⩾ n 0
.
In simple terms, we want to find a function
g ( n ) g(n) g ( n )
that is always going to be equal to or greater than
f ( n ) f(n) f ( n )
when multiplied by a constant for large values of
n n n
.
Example:
f ( n ) = 2 n + 3 f(n) = 2n + 3 f ( n ) = 2 n + 3
can be written as
O ( n ) O(n) O ( n )
after ignoring co-efficient of highest-growing term and lower-order terms.
Since
f ( n ) ⩽ O ( g ( n ) f(n) \leqslant O(g(n) f ( n ) ⩽ O ( g ( n )
, equating it to above gives us
g ( n ) = n g(n) = n g ( n ) = n
.
Let’s prove it mathematically:
f ( n ) ⩽ c g ( n ) ∀ n ⩾ n 0 i.e. ( 2 n + 3 ) ⩽ c g ( n ) i.e. ( 2 n + 3 ) ⩽ c n ∵ g ( n ) = n f(n) \leqslant cg(n) \space \forall \space n \geqslant n_0 \\
\text{i.e.}\space(2n + 3) \leqslant cg(n) \\
\text{i.e.}\space(2n + 3) \leqslant cn \space \because g(n) = n f ( n ) ⩽ c g ( n ) ∀ n ⩾ n 0 i.e. ( 2 n + 3 ) ⩽ c g ( n ) i.e. ( 2 n + 3 ) ⩽ c n ∵ g ( n ) = n
Quick way to find the value of c is take leading constant of highest growing term and add 1 .
∴ c = 3 Substituting c to find the value of n 0 2 n + 3 ⩽ 3 n 3 ⩽ n ∴ n 0 = 3 \therefore c = 3 \\
\small \text{Substituting} \space c \space \text{to find the value of } n_0 \\
2n + 3 \leqslant 3n \\
3 \leqslant n \therefore n_0 = 3 \\ ∴ c = 3 Substituting c to find the value of n 0 2 n + 3 ⩽ 3 n 3 ⩽ n ∴ n 0 = 3
So for all values of
n ⩾ 3 n \space \geqslant 3 n ⩾ 3
, the equation
2 n + 3 ⩽ 3 n 2n+3 \leqslant 3n 2 n + 3 ⩽ 3 n
holds true.
If we try putting some values, say
n = 4 n = 4 n = 4
in above equation, we can observe it holds true. Hence proved.
Some more examples:
{ n 4 , 2 n + 3 , n 100 + log n , 100 , log n , . . . } ∈ O ( n ) \{\frac{n}{4}, 2n + 3, \frac{n}{100} + \log n, 100, \log n, ...\} \in O(n) { 4 n , 2 n + 3 , 100 n + log n , 100 , log n , ... } ∈ O ( n )
{ n 2 + n , 2 n 2 , n 2 100 , . . . } ∈ O ( n 2 ) \{n^2 + n, 2n^2, \frac{n^2}{100}, ...\} \in O(n^2) { n 2 + n , 2 n 2 , 100 n 2 , ... } ∈ O ( n 2 )
Since Big O is upper bound, all functions in 1 can be said to belong to 2, but it helps to use tight bounds .
Big O gives the upper bound . If we say an algorithm is linear, then the algorithm in question is
⩽ O ( n ) \leqslant O(n) ⩽ O ( n )
. So, it's going to perform linearly in worst case scenario or better. Therefore Big O is the upper bound of the algorithm.
f ( n ) = Ω ( g ( n ) ) f(n) = \Omega(g(n)) f ( n ) = Ω ( g ( n ))
iff there are exact constants
c c c
and
n 0 n_0 n 0
such that
0 ⩽ c g ( n ) ⩽ f ( n ) 0 \leqslant cg(n) \leqslant f(n) 0 ⩽ c g ( n ) ⩽ f ( n )
for all
n ⩾ n 0 n \geqslant n_0 n ⩾ n 0
.
Big Omega is exact opposite of Big O.
Big Omega gives the lower bound of an algorithm i.e. the algorithm will perform at least or better than it.
Example -
f ( n ) = 2 n + 3 = Ω ( n ) f(n) = 2n + 3 = \Omega(n) f ( n ) = 2 n + 3 = Ω ( n )
{ n 4 , n 2 , 2 n , 2 n + 3 , n 2 . . . } ∈ Ω ( n ) \{\frac{n}{4}, \frac{n}{2}, 2n, 2n+3, n^2 ...\} \in \Omega(n) { 4 n , 2 n , 2 n , 2 n + 3 , n 2 ... } ∈ Ω ( n )
i.e. all the functions having order of growth greater than or equal to linear.
If
f ( n ) = Ω ( g ( n ) ) t h e n g ( n ) = O ( f ( n ) ) f(n) = \Omega(g(n)) \space \small{then} \space g(n) = O(f(n)) f ( n ) = Ω ( g ( n )) t h e n g ( n ) = O ( f ( n ))
.
f ( n ) = Θ ( g ( n ) ) f(n) = \Theta(g(n)) f ( n ) = Θ ( g ( n ))
iff there are exact constants
c 1 , c 2 , n 0 c_1, c_2, n_0 c 1 , c 2 , n 0
such that
0 ⩽ c 1 g ( n ) ⩽ f ( n ) ⩽ c 2 g ( n ) f o r a l l n ⩾ n 0 0 \leqslant c_1g(n) \leqslant f(n) \leqslant c_2g(n) \space \small{for all} \space n \geqslant n_0 0 ⩽ c 1 g ( n ) ⩽ f ( n ) ⩽ c 2 g ( n ) f or a ll n ⩾ n 0
.
Big Theta gives the exact bound on the order of growth of a function.
Example - For
f ( n ) = 2 n + 3 = Θ ( n ) f(n) = 2n + 3 = \Theta(n) f ( n ) = 2 n + 3 = Θ ( n )
If
f ( n ) = Θ ( g ( n ) ) f(n) = \Theta(g(n)) f ( n ) = Θ ( g ( n ))
then
f ( n ) = O ( g ( n ) ) and f ( n ) = Ω ( g ( n ) ) g ( n ) = O ( f ( n ) ) and g ( n ) = Ω ( f ( n ) ) f(n) = O(g(n)) \text { and } f(n) = \Omega(g(n)) \\
g(n) = O(f(n)) \text { and } g(n) = \Omega(f(n)) f ( n ) = O ( g ( n )) and f ( n ) = Ω ( g ( n )) g ( n ) = O ( f ( n )) and g ( n ) = Ω ( f ( n ))
{ n 2 4 , n 2 2 , n 2 , 4 n 2 , . . . } ∈ Θ ( n 2 ) \{\frac{n^2}{4}, \frac{n^2}{2}, n^2, 4n^2, ...\} \in \Theta(n^2) { 4 n 2 , 2 n 2 , n 2 , 4 n 2 , ... } ∈ Θ ( n 2 )
We should use big 𝛳 notation whenever possible.